Blogpost vom 11. Juli 2017
k-Means-Clustering: Big Data am Beispiel von Hemdgrößen
An dieser Stelle wollen wir uns dem Thema Big Data einmal auf ganz praktische Weise nähern – am Beispiel von Kleidungsstücken, mit Hilfe von k-Means-Clustering.
Sagen wir, Micromata möchte allen Mitarbeitern Hemden mit dem neuen Firmenlogo schenken. Frei nach dem Motto “individuelle Software und individuelle Kleidung” sollen die Hemden den Mitarbeitern möglichst gut passen. Gleichzeitig ist eine Maßanfertigung für jeden einzelnen Mitarbeiter zu aufwendig. Als Kompromiss sollen Hemden in den Größen S, M und L anhand von Referenzmitarbeitern für die jeweiligen Größen maßgeschneidert werden.
Mit Hilfe des k-Means-Clustering-Algorithmus sollen dafür automatisch die drei Mitarbeiter, welche die entsprechenden Hemd-Größen am besten repräsentieren, ausgewählt werden. Auf Grundlage ihrer Maße können die neuen Hemden so gefertigt werden, dass diese dann vielen Mitarbeitern möglichst gut passen.
Daten sammeln
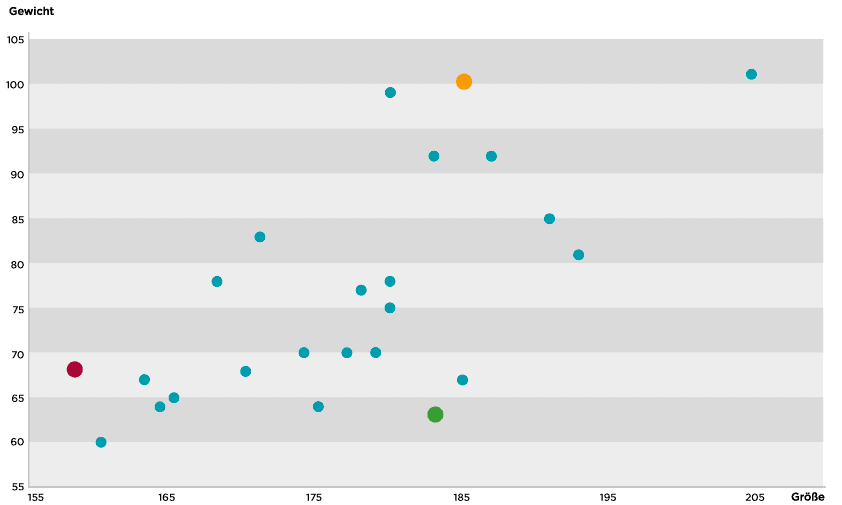
Um einen Überblick über die Proportionen der Mitarbeiter zu erhalten, werden diese nach ihrer Größe und ihrem Gewicht befragt. Zur Vereinfachung unseres Beispiels unterscheiden wir dabei nicht zwischen Männern und Frauen. Die genannten Angaben tragen wir für eine erste Veranschaulichung in ein Diagramm ein (siehe Abbildung 1).
Dr. Michael Lesniak
Softwareentwicklung
Die Idee
Wir wollen die Daten der Mitarbeiter drei Gruppen für die unterschiedlichen Hemdgrößen zuordnen. Jede Gruppe wird durch einen ihr zugehörigen Mittelpunkt repräsentiert. Das Ziel des k-Means-Clustering-Algorithmus ist das automatische Berechnen dieser k-Mittelpunkte (sog. Cluster-Mittelpunkte), welche die bekannten Daten am besten repräsentieren. In unserem Fall ist k = 3, da wir drei verschiedene Hemdgrößen herstellen lassen wollen.
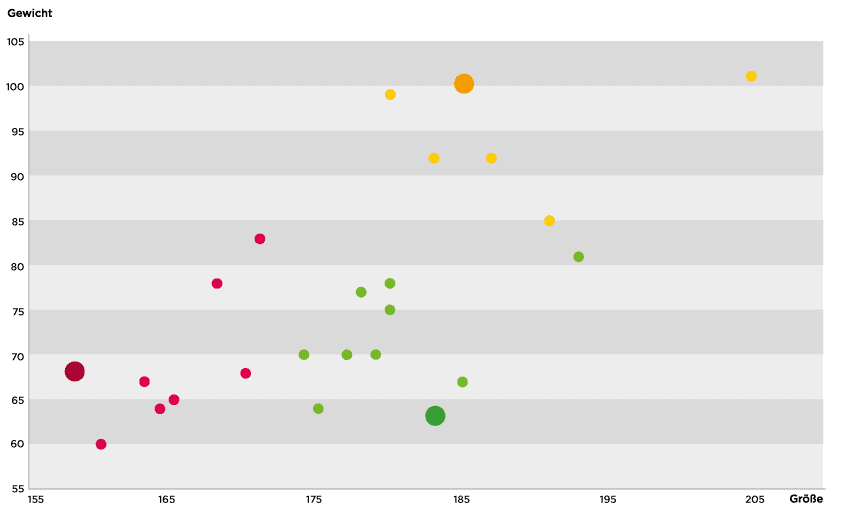
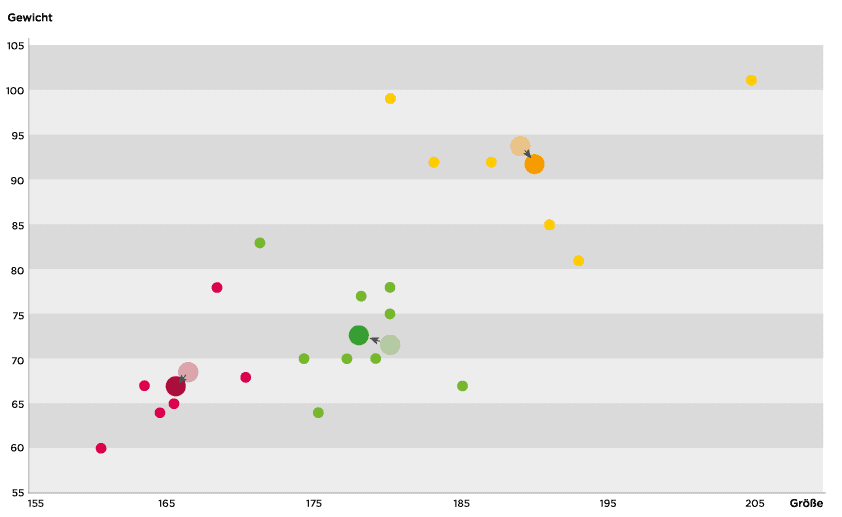
Zu Beginn der Berechnung werden drei zufällig gewählte Mittelpunkte gewählt und in unserer Veranschaulichung eingetragen (siehe Abbildung 2).
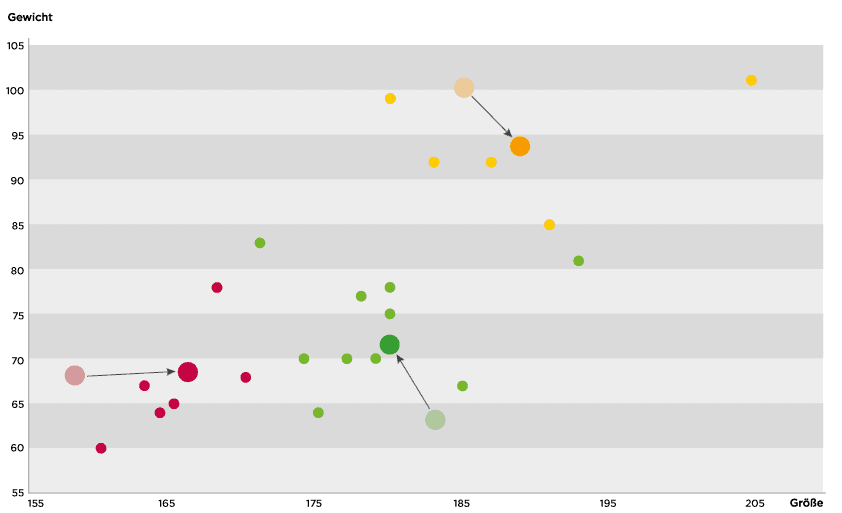
Anschließend wird jeder Messwert dem am nächsten liegenden Cluster-Mittelpunkt zugeordnet. Für das obige Beispiel ergibt sich die in Abbildung 3 gezeigte Zuordnung.
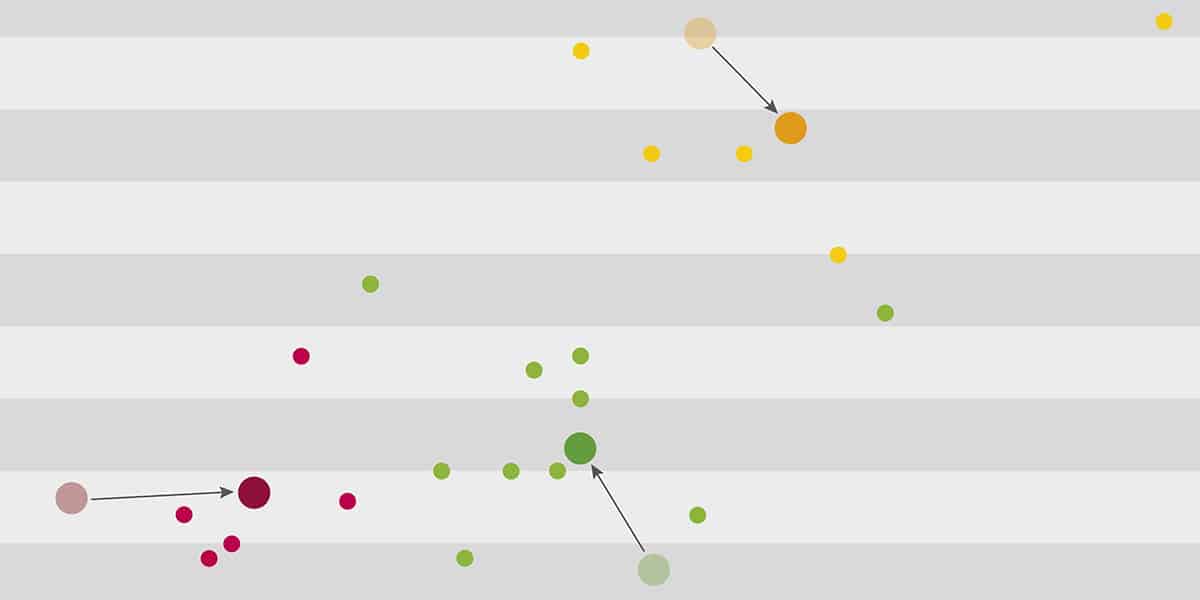
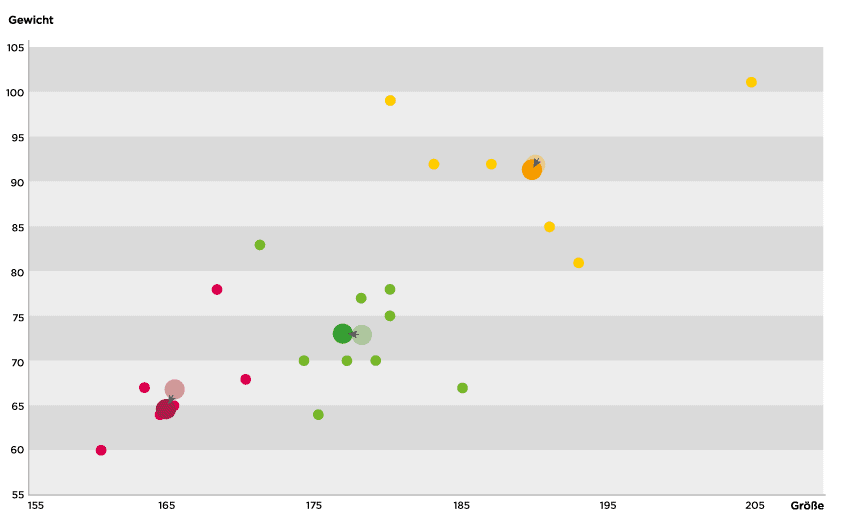
Für jeden Mittelpunkt wird nun das geometrische Zentrum seiner ihm zugeordneten Messwerte ermittelt. Dorthin wird der Mittelpunkt verschoben (siehe Abbildung 4).
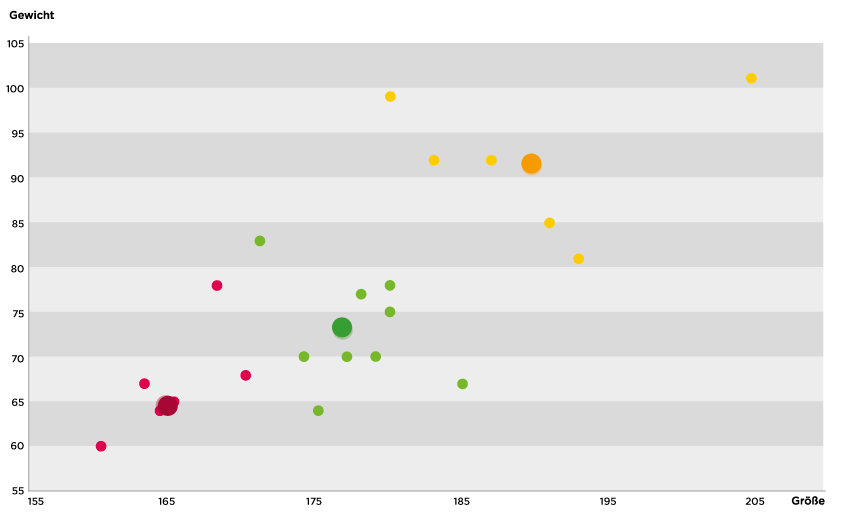
Ergebnisse nutzen
Wir haben nun die besten Durchschnittsgrößen gefunden, wenn wir unsere Mitarbeiter in drei Größenklassen teilen. Da nicht genau an jedem Mittelpunkt ein Datensatz vorhanden ist, wird der geometrisch jeweils am nächsten liegende Datensatz verwendet. An diesem Mitarbeiter wird die Referenz für die entsprechende Hemdgröße gemessen. Jeder Mitarbeiter kann sich nun ein Hemd in seiner Größe aussuchen.
Und in der Realität?
Der k-Means-Clustering-Algorithmus sieht auf den ersten Blick sehr einfach aus. Gleichzeitig ist seine Anwendung in der Realität hilfreich und sein Nutzen mächtig. Im Folgenden gehen wir kurz auf einige Herausforderungen ein, die sich im Kontext seines Einsatzes ergeben.
- In echten Fällen nutzen wir häufig wesentlich mehr als zwei Daten-Dimensionen. Es ist nicht ungewöhnlich, dass ein einzelner Datensatz aus zehn und mehr Komponenten besteht – was die Visualisierung und Anschaulichkeit an dieser Stelle allerdings enorm erschwert hätte.
- In unserem Beispiel war die Anzahl k der Mittelpunkte vorgegeben. In der Praxis ist die Anzahl nicht immer klar spezifiziert. Dieser Herausforderung begegnen wir mit geschicktem Ausprobieren, d. h. es werden verschiedene Werte für k systematisch getestet und die jeweilige Güte der Lösung bewertet.
- Die Mittelpunkte in unserem Beispiel wurden iterativ angepasst und verbessert. Nach wenigen Schritten gab es keine großen Sprünge mehr und passende Mitarbeiter zum Maßnehmen waren schnell gefunden. In der Praxis können bis zur Lösungsfindung Millionen Schritte nötig sein. Wenngleich es mathematisch keinen Unterschied macht, ist der dafür benötigte Rechenaufwand natürlich wesentlich größer.
Trotz der genannten Randbedingungen ist k-Means-Clustering ein sehr nützliches und vor allem effizient nutzbares Werkzeug im Big-Data-Baukasten: Dank moderner Frameworks wie Hadoop und Spark sind eine hohe Dimensionsanzahl, unklare k und viele Iterationen durchaus beherrschbare Herausforderungen.
Und in Ihrer Praxis?
In Ihrem Alltag beschäftigen Sie sich eher selten mit der Ermittlung passender Hemdgrößen. Daher stellen wir in diesem Abschnitt drei Szenarien vor, auf die sich der kMCA anwenden lässt.
Szenario 1: Produktionsstandards
In der Produktion von Waren ist das Einhalten von Qualitätsstandards häufig eines der wichtigsten Primärziele. Gleichzeitig sind Schwankungen in den einzuhaltenden Messwerten erlaubt bzw. aufgrund der Messtechniken nicht vermeidbar. Mit Hilfe des kMCA können verschiedene Messwerte als einzelne Datendimensionen interpretiert werden. Die ermittelten Cluster-Mittelpunkte entsprechen unterschiedlichen Qualitätsstufen. Zum einen ist damit eine automatische Zuordnung eines Produkts zu einer bestimmten Qualitätsstufe, z. B. für unterschiedliche Preise, möglich, zum anderen auch die Erkennung von Fehlproduktionen, die keiner Stufe sinnvoll zugeordnet werden können.
Szenario 2: Kundengruppen
Bei der Einteilung von Kunden, z. B. in der Kampagnenplanung im Werbebereich, ist häufig nicht klar, wie neue Kunden aufgrund demografischer oder ökonomischer Kriterien eingeordnet werden können. Über die automatische Clusterbildung durch bestehende Kundendaten kann ein Interessent in verschiedene Kategorien, im Bereich Automotive beispielsweise Sportwagen, Familienvan, Citysprinter usw. eingestuft werden. Durch diese automatische Einstufung sind gezieltere Werbemaßnamen möglich.
Szenario 3: Sicherheit
Das Erkennen von Betrugsversuchen und ungewöhnlichem, potentiell gefährdendem Verhalten, spielt in vielen Systemen eine immer größere Rolle. Gleichzeitig ist eine vollständige manuelle Überprüfung des Kundenverhaltens und aller Datenströme aufgrund der großen Datenmengen nicht mehr realistisch. Über k-Means-Clustering können Kunden aufgrund ihres maschinell beobachteten Verhaltens in verschiedene Gefahren-Kategorien zugeordnet und entsprechende Maßnahmen eingeleitet werden.
Fazit
Wir hoffen, dieses Beispiel hat Ihnen gezeigt, wie einer der bekanntesten Klassifizierungsalgorithmen aus dem Big-Data-Baukasten, namentlich das k-Means-Clustering, funktioniert. Durch die Implementierung in entsprechenden Frameworks (z. B. Hadoop und Spark) lässt sich dieser Analyseansatz für große Datenmengen performant nutzen, so dass auch aus Ihren Daten interessante und nutzbringende Erkenntnisse gezogen werden können.